课上学了一种大数据计算相似性的算法,觉得很巧妙,在这里总结下。
使用场景
求相似性的场景有很多,比如比较两图相似性从而做一些处理,或者搜索引擎比较文本相似性从而确定返回的搜索结果等等。这种场景常常面临的问题是要进行比较的数据特征量非常大,同时比较对象又非常多,不能直接比较。LSH正是解决了这个问题。
LSH流程
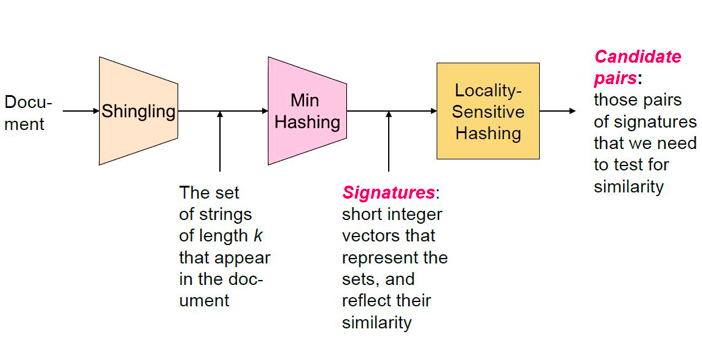
LSH分为三步:
- Shingling: Convert documents to sets
- Min Hashing: Convert large sets to short signatures, while preserving similarity
- Locality Sensitive Hashing: Focus on pairs of signatures likely to b from similar documents - Candidate pairs!
要测相似性就要确定距离/相似性函数,LSH使用的是jaccard距离/相似性,具体如下:
- sim(C1,C2) = | C1 ∩ C2 | / | C1 U C2 |
- d(C1,C2) = 1 - | C1 ∩ C2 | / | C1 U C2 |
第一步:Shingling
Shingling是将整个文档转化为一个set,这里我们不重视文档顺序、重要词等信息,所以shingling是最好选择。
K-shingle(k-gram)则是将文档分成以k个token为一个单位的序列,token可以是字符、单词或者其他。例如k=2,则对于文档D = abcab,2-shingle的set则是:C = S(D) = {ab, bc, ca}。k的取值:
- k = 5,对于比较短的文章
- k = 10,对于很长的文章
随后可以将每一个shingle作为一个维度将所有文档联合起来构建一个0/1矩阵,这个 矩阵:
- Rows = elements (shingles)
- Columns = set(documents)
例如:
| C1 | C2 | C3 | C4 | |
|---|---|---|---|---|
| Shingles1 | 1 | 1 | 1 | 0 |
| Shingles2 | 1 | 1 | 0 | 1 |
| … | 0 | 1 | 0 | 1 |
| … | 0 | 0 | 0 | 1 |
很显然这个矩阵非常稀疏的。这样计算量非常大,所以有第二步来“压缩矩阵”。
第二步:Minhash
minhash需要压缩矩阵,将原来100,000维的压缩到100维,采用了很聪明的方法:概率聚类大法!
具体描述:将上述矩阵每一列随机排列,然后记录第一个1的对应位置(位置标注方式不一定是递增序列,而和产生随机的方式有关)
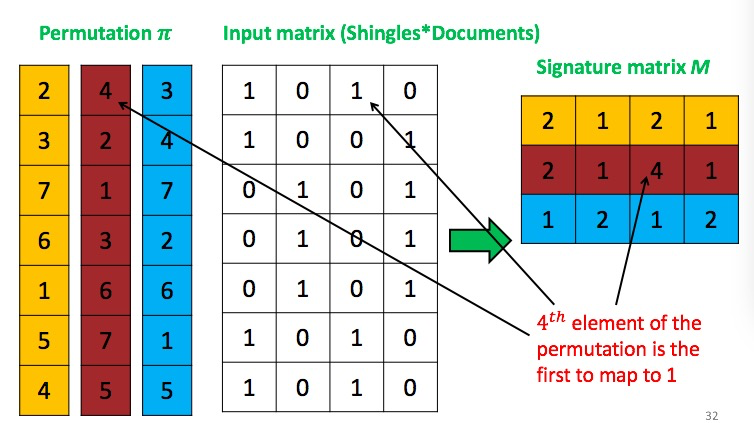
每一次随机都会产生1个signature,100次随机就针对每个文档产生一个长度100的signature,文档之前只要互相比较一下这个signature的相似性就相当于比较文档的相似性。
这个算法的可行性用公式表达则是:
- Pr[ min( π (C1 )) = min ( π (C2 )) ] = sim(C1,C2)
这个结论是可以证明的,此处略过。
由于这里要随机100次,这个显然是比较麻烦的,所以随机用hash方法来进行。
全局hash为:
- h_a,b(x) = (( a*x + b )mod p ) mod N
然后每次只要随机产生a,b两个值就好。之后按照产生的hash函数的大小顺序进行排列。hash产生重复的值也不要紧,signature就是产生的这个hash值即可。
这里解决了维度太多的问题,但相互比较问题还是没解决,因为文档很多,所以要非常多次比较。第三步将减少比较流程,只要候选文档之间相互比较即可。
第三步:Locality Sensitive Hashing
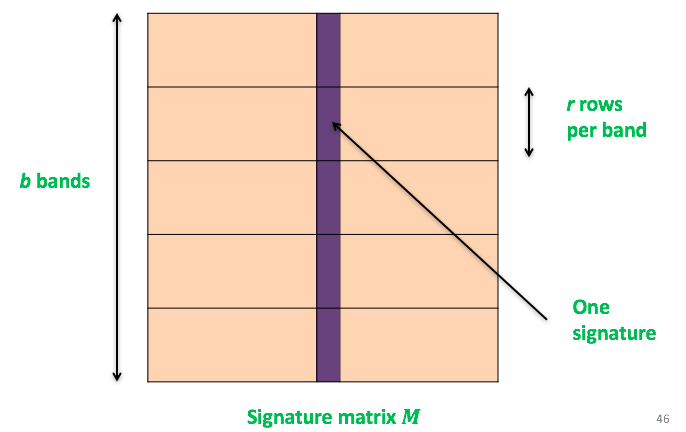
这里先讲M矩阵分成了b个bands,每个bands里包含r行,如图:
之后再对每个内容进行hash,使其map到k个buckets中,如果C1,C2有大于等于一个band在同一buckets中,则对他们进行比较,如图:
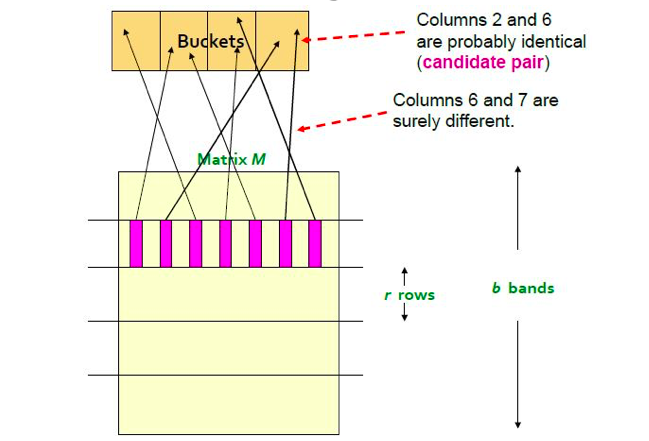
这样将每个bands都map到Buckets的不同块里,如果map到同一个buckets的块里,则称为candidate pair,他们不一定相等,要进行比较。但如果map到不同的块里,表明这两个band一定不同,不需要进行比较。
下面验证一下这个算法的可行性。
假设C1和C2的相似度为t,b为bands数目,r为每个band多少row,可以得知:
- band中所有row相等(该band会映射到同一bucket块)概率: t^r
- band中row存在不相等row概率:1-t^r
- 没有一个band是相等的概率:(1 - t^r)^b
- 至少有一个band相等的概率:1 - (1 - t^r)^b
按照公式计算,当b取20,r取5,对于相似度30%的文档C1,C2(不希望有bands出现在同一buckets中),有4.7%的几率至少一个bands分在同一buckets中,我们花多余的代价去计算它概率比较小。而相对于相似度80%的文档,有99.96%的几率我们要去比较他们,我们会错过一对相似文档的概率不到0.04%,可以接受。
综上改算法是可行的。