流数据,顾名思义,就是针对流数据(例如google查询、twitter的状态更新这类数据)的一些挖掘。不同于普通数据集,流数据源源不断地产生,而我们的存储空间是有限的。所以要采取一些办法,:
- Samping data from stream
- Queries over sliding windows
- Filtering a data streaming
Sampling data from stream
由于我们不能存储整个stream,所以要存一些sample,具体有两种方式
- Sample一个stream的固定比例
- 维护一个固定大小的随机Sample —— 蓄水池采样
固定比例
以用户的查询为例:假设有s个单次查询,有d个两次查询,即总共有s+2d次查询,sample率为p(0<p<=1),求用户两次查询的比例
正确答案:d/(s+d)
按照条件推倒:dp^2/(sp+dp^2+2p(1-p)d)
这个准确率问题还是比较大的,为了改良,可以采用以取用户sample的方式。
固定大小的sample —— 蓄水池采样
很好玩的问题:假如有一本非常厚的电话簿,你要随机挑1000个人打电话,并且保证每个人被选中的几率相等,你要怎么做?
这里的电话簿就像数据流,你不能先数一遍总共有多少人,再产生一千个随机数这样,效率太低。
解决方法:
先选前1000人,然后后面的每一位以k/n的概率决定替换掉前面的任意一位。其中n是当前总共人数,k是蓄水池大小。例如第1001位就有1000/1001的概率替换掉前面1000个人中任意一个。
证明:
条件: sample size: k,total size: n,probability of each element: s/n
求证: 对于n->n+1的情况,probability of each element: k/n+1,即无论n多大,每个元素被选中概率均等
证明:
每个元素被选中概率:k/n
n->n+1后,每个被替换前面概率:k/n+1
而假设A而原来在sample里的,仍然还在的概率为: (1-k/n+1) + (k/n+1)*(k-1/k) = n/n+1,这个公式前者是n+1这个元素没被选中,后者是没替换自己的概率
那么A的概率就是:k/n * n/n+1 = k/n+1
综上,概率相等~
Sliding Windows
就是滑动窗口,简单来说:最多储存N bits,当又来一个新bit时,吐出第N+1个bits(也就是窗口里最老的那个)。
问题:如果我们要统计N中有一个1,那必须全部存储N中的内容,但窗口的存储空间有限,因此这里用了DGIM方法->exponential Window。
DGIM算法
它是通过Bucket来对滑动窗口进行划分,每个桶包括:
- 桶最右边的timestamp(O(logN) bits)
- 在每个桶中1刀数量(O(log logN)bits)
桶的限制:每个桶里的1的数量是2的次方。
桶的特征:
- 只有1个或者2个桶有相同数目的2的次方个1
- 桶和桶的timestamps不会重叠
- 桶是按照大小有序的
- 当桶的end-time > N的时候(即整个桶已经从窗口中走了),桶会消失
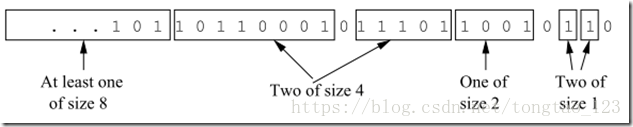
DGIM算法中数据结构的更新(2048式更新):
- 每一个新的位进入滑动窗口后,最左边一个位从窗口中移出(同时从桶中移出);如果最左边的桶的时间戳是当前时间戳减去N(也就是说桶里已经没有处于窗口中的位),则放弃这个桶;
- 对于新加入的位,如果其为0,则无操作;否则建立一个包含新加入位的大小为1的桶;
- 由于新增一个大小为1的桶而出现3个桶大小为1,则合并最左边的两个桶为一个大小为2的桶;合并之后可能出现3个大小为2的桶,则合并最左边两个大小为2的桶得到一个大小为4的桶……依次类推直到到达最左边的桶。
如何估计最新N窗口中1的数目呢?
- 将除了最后一个的所有的bucket大小(这里大小都是指1的数目)加起来
- 再加上最后一个bucket的一半大小
准确率:>= 50%
Filtering Data Streams
问题:垃圾邮件的过滤问题,我们知道有10亿个好的email address,如果邮件来自这些address,那么它就不是spam。即现在有一封邮件{“address”:”contents”},如果key可以匹配10亿email address就不是spam。
Bloom Filter
设S是刚刚好的email address集合,而B是大小为n,全部初始化为0的一个bit array

使用k个相互独立的hash函数h1,h2……hk,他们可以将元素映射到[0,n]的bit array上。将S中元素通过k个hash函数映射,映射到的地方设置为1
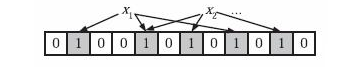
这里的x1,x2就是S的元素。
当判断一个元素y1,y2是否在集合S中时,就通过相同的hash函数将其映射到B上,如果任何一个hash函数映射到的地方存在0,那y就不在S中,反之则证明在S上,或者是一个false positive(将错的分到对的里)。
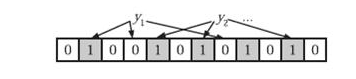
如图y1就不在S中,y2或是在S中,或是一个false positive。但这种方法不存在true negative(将对的分到错的里)。